In this paper, we show that the time dilation field of mass-energy is sufficient to predict gravitational effects on light. Essay written for the Gravity Research Foundation 2021 Awards for Essays on Gravitation.
Free-falling into Black Hole
We start with a black hole, B, possessing a Schwarzschild radius (rs) of 3000 m, giving it a mass of roughly one solar-mass (~2*10^30 kg). We take a body, A, of negligible mass, initially resting at a great distance (PEi = KEi = 0), and allow it to free-fall towards B.
To calculate A’s coordinate velocity at a given distance, r, from the center of B, we start with

(1)
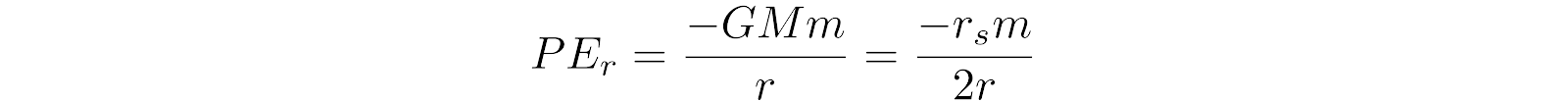
(2)
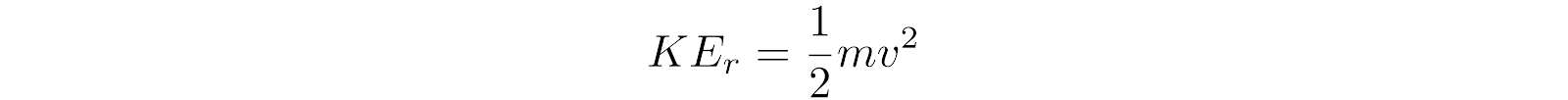
(3)
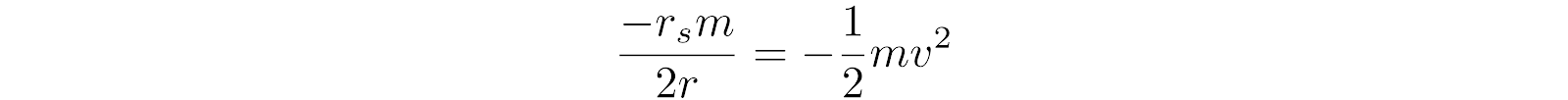
(4)
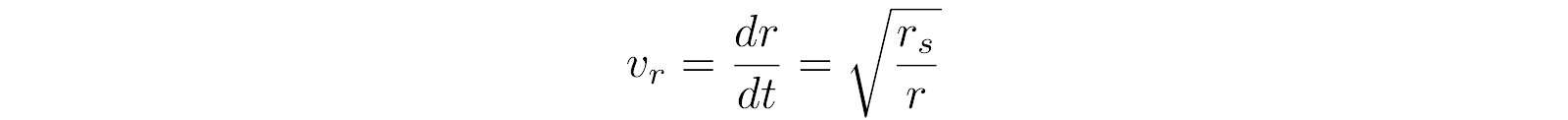
(5)
so

(6)
Integrating gives us:
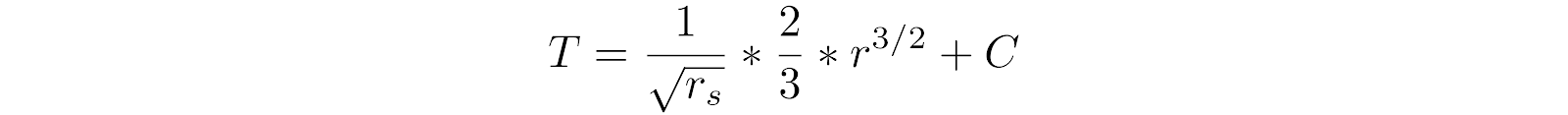
(7)
We evaluate the equation for the final 1000 meters of A’s path before reaching the event horizon (i.e. r = 4000..3000, see Fig 2)
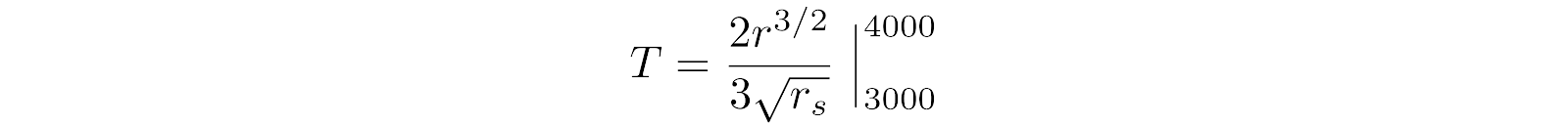
(8)
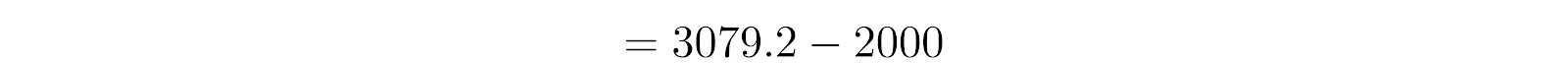
(9)
So

(10)
Here we take note of the proper velocity of A at r = 4000 (see Fig 2)
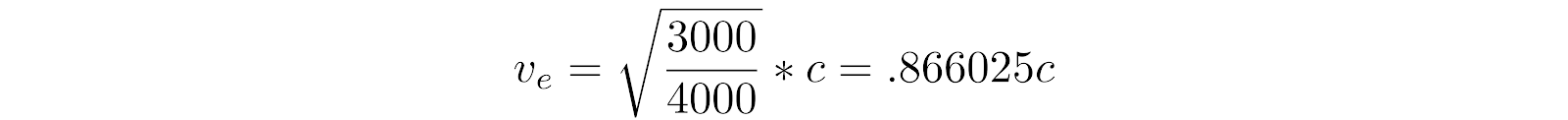
(11)
We also note that
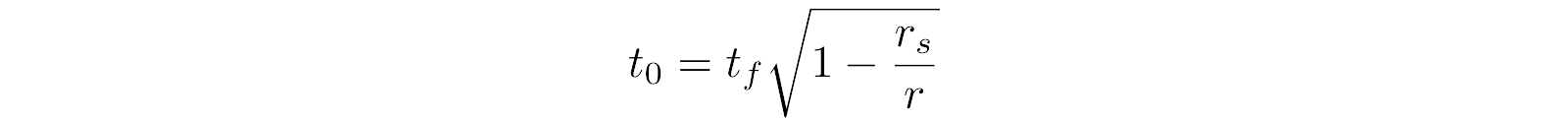
(12)
where t0 is the proper time of events for A, tf is the coordinate time of those same events (for a distant observer), and the radical value is the time dilation factor which approaches 0 as r approaches the event horizon at rs.

<continued...>
Free-falling into Black Hole
We start with a black hole, B, possessing a Schwarzschild radius (rs) of 3000 m, giving it a mass of roughly one solar-mass (~2*10^30 kg). We take a body, A, of negligible mass, initially resting at a great distance (PEi = KEi = 0), and allow it to free-fall towards B.
To calculate A’s coordinate velocity at a given distance, r, from the center of B, we start with
(1)
(2)
(3)
(4)
(5)
so
(6)
Integrating gives us:
(7)
We evaluate the equation for the final 1000 meters of A’s path before reaching the event horizon (i.e. r = 4000..3000, see Fig 2)
(8)
(9)
So
(10)
Here we take note of the proper velocity of A at r = 4000 (see Fig 2)
(11)
We also note that
(12)
where t0 is the proper time of events for A, tf is the coordinate time of those same events (for a distant observer), and the radical value is the time dilation factor which approaches 0 as r approaches the event horizon at rs.
<continued...>
