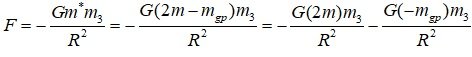icarus2
Registered Senior Member
One of humanity's ultimate questions is "How did the universe come into existence?"
Since energy is one of the most fundamental physical quantities in physics, and particles and the like can be created from this energy, this question is related to the question "How did energy come into existence?"
Cosmology can be largely divided into a model in which energy has continued to exist and a model in which energy is also created. Each model has its strengths and weaknesses, but in models that assume that some energy existed before our universe was born, "How did that energy come about?" The question still exists.
In order to explain the source of energy in our universe, there have been models that claim the birth of the universe from nothing, or a Zero Energy Universe. However, it lacks a specific mechanism for how beings were born out of nothing. Some models presuppose an Inflaton Field-like existence or are depicted in very poor condition. *The nothingness referred to here is not a complete nothingness, but a state of zero energy.
I would like to suggest a solution to this ultimate problem.
Let's look at the characteristics of gravitational potential energy first, and explain the mechanism of birth from nothing.
1. Changes in the range of gravitational interactions over time
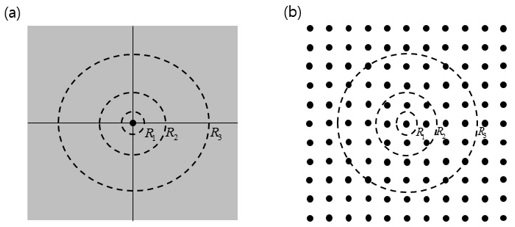
In Figure 1, if the mass or energy within the radius R_1 interacted gravitationally at t_1 (an arbitrary early time), the mass or energy within the radius R_2 will interact gravitationally at a later time t_2.
As the universe ages, the mass or energy involved in gravitational interactions changes, resulting in changes in the energy composition of the universe.
In the case of a uniform distribution, the total energy E_T of the system is
E_T= Σmc^2 + Σ-Gmm/r =Mc^2 - (3/5)GM^2/R
Since there is an attractive component (Mass energy) and a repulsive component (Gravitational potential energy or Gravitational self-energy), it contains elements that can explain the accelerated expansion and decelerated expansion of the universe.
U/E = {-(3/5)GM^2/R }/Mc^2 = -(4πGρ/5c^2)R^2 = -kR^2
In the case of a uniform distribution, comparing the magnitudes of mass energy and gravitational potential energy, it is in the form of -kR^2. That is, over time, it is possible for negative gravitational potential energy values to become greater than positive mass energy values.
2. The inflection point at which the magnitudes of mass energy and gravitational potential energy are equal
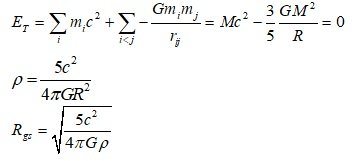
The inflection point is the transition from decelerated expansion to accelerated expansion.
If R < R_gs , then the positive energy is greater than the negative gravitational potential energy, so the mass distribution is dominated by attractive force and is decelerating.
If R > R_gs, then the negative gravitational potential energy is greater than the positive energy, so the mass distribution is dominated by the repulsive (anti-gravity) force and accelerated expansion.
So, if we connect R_gs with the birth of the universe, we have the potential to create the universe out of nothing, even the expansion of the universe.
3. Birth and Expansion of the Universe from the Uncertainty Principle
3.1 The Uncertainty Principle - Inflating in Planck time
ΔxΔp≥hbar/2
ΔtΔE≥hbar/2
During Planck time, fluctuations in energy
ΔE≥hbar/2Δt =(1/2)m_pc^2
The magnitude of the energy entering the accelerating expansion in Planck time is (5/6)m_pc^2.
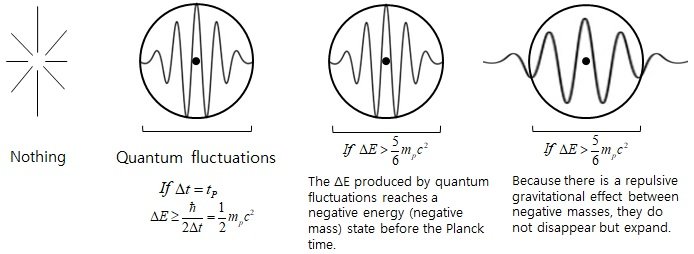
It means,
According to the uncertainty principle, it is possible to change (or create) more than (1/2)m_pc^2 energy during the Planck time,
If an energy change above (5/6)m_pc^2 that is slightly larger than the minimum value occurs, the total energy of the energy distribution reaches negative energy, i.e., the negative mass state, within the time Δt where quantum fluctuations can exist.
However, since there is a repulsive gravitational effect between negative masses, the corresponding mass distribution expands instead of contracting.(Stated another way, it expands because the repulsive force due to the negative gravitational self-energy is greater than the attractive force due to the positive energy (mass) distribution.) Thus, the quantum fluctuations generated by the uncertainty principle cannot return to nothing, but can expand and create the present universe.
3.2. The magnitude at which the minimum energy generated by the uncertainty principle equals the minimum energy required for accelerated expansion
In the above analysis, the minimum energy of quantum fluctuation possible during Planck time is ΔE≥(1/2)m_pc^2, and the minimum energy fluctuation for which expansion after birth can occur is ΔE≥(5/6)m_pc^2. Since (5/6)m_pc^2 is greater than (1/2)m_pc^2, the birth and coming into existence of the universe in Planck time is a probabilistic event.
For those unsatisfied with probabilistic event, consider the case where the birth of the universe was an inevitable event.
Letting Δt=kt_p, and doing some calculations, we get the k=(3/5)^(1/2)
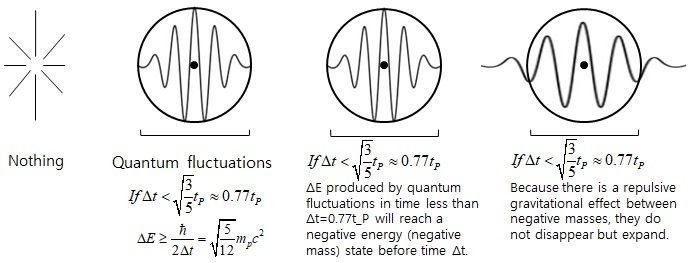
To summarize,
If Δt ≤ ((3/5)^(1/2))t_p, then ΔE ≥ ((5/12)^(1/2))m_pc^2 is possible. And, the minimum magnitude at which the energy distribution reaches a negative energy state by gravitational interaction within Δt is ΔE=((5/12)^(1/2))m_pc^2. Thus, when Δt < ((3/5)^(1/2))t_p, a state is reached in which the total energy is negative within Δt.
In other words, when quantum fluctuation occur where Δt is smaller than (3/5)^(1/2)t_p = 0.77t_p, the corresponding mass distribution reaches a state in which negative gravitational potential energy exceeds positive mass energy within Δt. Therefore, it can expand without disappearing.
In this case, the situation in which the universe expands after birth becomes an inevitable event.
[Abstract]
There was a model claiming the birth of the universe from nothing, but the specific mechanism for the birth and expansion of the universe was very poor.
According to the energy-time uncertainty principle, during Δt, an energy fluctuation of ΔE is possible, but this energy fluctuation should have reverted back to nothing. By the way, there is also a gravitational interaction during the time of Δt, and if the negative gravitational self-energy exceeds the positive mass-energy during this Δt, the total energy of the corresponding mass distribution becomes negative energy, that is, the negative mass state. Because there is a repulsive gravitational effect between negative masses, this mass distribution expands. Thus, it is possible to create an expansion that does not go back to nothing.
Calculations show that if the quantum fluctuation occur for a time less than Δt = ((3/10)^(1/2))t_p ~ 0.77t_p, then an energy fluctuation of ΔE > ((5/6}^(1/2))m_pc^2 ~ 0.65m_pc^2 must occur. But in this case, because of the negative gravitational self-energy, ΔE will enter the negative energy (mass) state before the time of Δt. Because there is a repulsive gravitational effect between negative masses, ΔE cannot contract, but expands. Thus, the universe does not return to nothing, but can exist.
Gravitational Potential Energy Model provides a means of distinguishing whether the existence of the present universe is an inevitable event or an event with a very low probability. And, it presents a new model for the process of inflation, the accelerating expansion of the early universe. This mechanism also provides an explanation for why the early universe started out in a high dense state. Additionally, when the negative gravitational potential energy exceeds the positive mass energy, it can produce an accelerated expansion of the universe. Through this mechanism, inflation, which is the accelerated expansion of the early universe, and dark energy, which is the cause of the accelerated expansion of the recent universe, can be explained at the same time.
# The Birth Mechanism of the Universe from Nothing and New Inflation Mechanism
https://www.researchgate.net/publication/371951438
# Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field
https://www.researchgate.net/publication/360096238
Since energy is one of the most fundamental physical quantities in physics, and particles and the like can be created from this energy, this question is related to the question "How did energy come into existence?"
Cosmology can be largely divided into a model in which energy has continued to exist and a model in which energy is also created. Each model has its strengths and weaknesses, but in models that assume that some energy existed before our universe was born, "How did that energy come about?" The question still exists.
In order to explain the source of energy in our universe, there have been models that claim the birth of the universe from nothing, or a Zero Energy Universe. However, it lacks a specific mechanism for how beings were born out of nothing. Some models presuppose an Inflaton Field-like existence or are depicted in very poor condition. *The nothingness referred to here is not a complete nothingness, but a state of zero energy.
I would like to suggest a solution to this ultimate problem.
Let's look at the characteristics of gravitational potential energy first, and explain the mechanism of birth from nothing.
1. Changes in the range of gravitational interactions over time

In Figure 1, if the mass or energy within the radius R_1 interacted gravitationally at t_1 (an arbitrary early time), the mass or energy within the radius R_2 will interact gravitationally at a later time t_2.
As the universe ages, the mass or energy involved in gravitational interactions changes, resulting in changes in the energy composition of the universe.
In the case of a uniform distribution, the total energy E_T of the system is
E_T= Σmc^2 + Σ-Gmm/r =Mc^2 - (3/5)GM^2/R
Since there is an attractive component (Mass energy) and a repulsive component (Gravitational potential energy or Gravitational self-energy), it contains elements that can explain the accelerated expansion and decelerated expansion of the universe.
U/E = {-(3/5)GM^2/R }/Mc^2 = -(4πGρ/5c^2)R^2 = -kR^2
In the case of a uniform distribution, comparing the magnitudes of mass energy and gravitational potential energy, it is in the form of -kR^2. That is, over time, it is possible for negative gravitational potential energy values to become greater than positive mass energy values.
2. The inflection point at which the magnitudes of mass energy and gravitational potential energy are equal
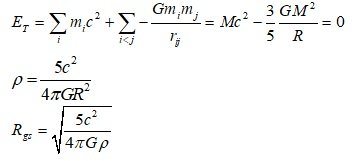
The inflection point is the transition from decelerated expansion to accelerated expansion.
If R < R_gs , then the positive energy is greater than the negative gravitational potential energy, so the mass distribution is dominated by attractive force and is decelerating.
If R > R_gs, then the negative gravitational potential energy is greater than the positive energy, so the mass distribution is dominated by the repulsive (anti-gravity) force and accelerated expansion.
So, if we connect R_gs with the birth of the universe, we have the potential to create the universe out of nothing, even the expansion of the universe.
3. Birth and Expansion of the Universe from the Uncertainty Principle
3.1 The Uncertainty Principle - Inflating in Planck time
ΔxΔp≥hbar/2
ΔtΔE≥hbar/2
During Planck time, fluctuations in energy
ΔE≥hbar/2Δt =(1/2)m_pc^2
The magnitude of the energy entering the accelerating expansion in Planck time is (5/6)m_pc^2.

It means,
According to the uncertainty principle, it is possible to change (or create) more than (1/2)m_pc^2 energy during the Planck time,
If an energy change above (5/6)m_pc^2 that is slightly larger than the minimum value occurs, the total energy of the energy distribution reaches negative energy, i.e., the negative mass state, within the time Δt where quantum fluctuations can exist.
However, since there is a repulsive gravitational effect between negative masses, the corresponding mass distribution expands instead of contracting.(Stated another way, it expands because the repulsive force due to the negative gravitational self-energy is greater than the attractive force due to the positive energy (mass) distribution.) Thus, the quantum fluctuations generated by the uncertainty principle cannot return to nothing, but can expand and create the present universe.
3.2. The magnitude at which the minimum energy generated by the uncertainty principle equals the minimum energy required for accelerated expansion
In the above analysis, the minimum energy of quantum fluctuation possible during Planck time is ΔE≥(1/2)m_pc^2, and the minimum energy fluctuation for which expansion after birth can occur is ΔE≥(5/6)m_pc^2. Since (5/6)m_pc^2 is greater than (1/2)m_pc^2, the birth and coming into existence of the universe in Planck time is a probabilistic event.
For those unsatisfied with probabilistic event, consider the case where the birth of the universe was an inevitable event.
Letting Δt=kt_p, and doing some calculations, we get the k=(3/5)^(1/2)

To summarize,
If Δt ≤ ((3/5)^(1/2))t_p, then ΔE ≥ ((5/12)^(1/2))m_pc^2 is possible. And, the minimum magnitude at which the energy distribution reaches a negative energy state by gravitational interaction within Δt is ΔE=((5/12)^(1/2))m_pc^2. Thus, when Δt < ((3/5)^(1/2))t_p, a state is reached in which the total energy is negative within Δt.
In other words, when quantum fluctuation occur where Δt is smaller than (3/5)^(1/2)t_p = 0.77t_p, the corresponding mass distribution reaches a state in which negative gravitational potential energy exceeds positive mass energy within Δt. Therefore, it can expand without disappearing.
In this case, the situation in which the universe expands after birth becomes an inevitable event.
[Abstract]
There was a model claiming the birth of the universe from nothing, but the specific mechanism for the birth and expansion of the universe was very poor.
According to the energy-time uncertainty principle, during Δt, an energy fluctuation of ΔE is possible, but this energy fluctuation should have reverted back to nothing. By the way, there is also a gravitational interaction during the time of Δt, and if the negative gravitational self-energy exceeds the positive mass-energy during this Δt, the total energy of the corresponding mass distribution becomes negative energy, that is, the negative mass state. Because there is a repulsive gravitational effect between negative masses, this mass distribution expands. Thus, it is possible to create an expansion that does not go back to nothing.
Calculations show that if the quantum fluctuation occur for a time less than Δt = ((3/10)^(1/2))t_p ~ 0.77t_p, then an energy fluctuation of ΔE > ((5/6}^(1/2))m_pc^2 ~ 0.65m_pc^2 must occur. But in this case, because of the negative gravitational self-energy, ΔE will enter the negative energy (mass) state before the time of Δt. Because there is a repulsive gravitational effect between negative masses, ΔE cannot contract, but expands. Thus, the universe does not return to nothing, but can exist.
Gravitational Potential Energy Model provides a means of distinguishing whether the existence of the present universe is an inevitable event or an event with a very low probability. And, it presents a new model for the process of inflation, the accelerating expansion of the early universe. This mechanism also provides an explanation for why the early universe started out in a high dense state. Additionally, when the negative gravitational potential energy exceeds the positive mass energy, it can produce an accelerated expansion of the universe. Through this mechanism, inflation, which is the accelerated expansion of the early universe, and dark energy, which is the cause of the accelerated expansion of the recent universe, can be explained at the same time.
# The Birth Mechanism of the Universe from Nothing and New Inflation Mechanism
https://www.researchgate.net/publication/371951438
# Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field
https://www.researchgate.net/publication/360096238
Last edited: