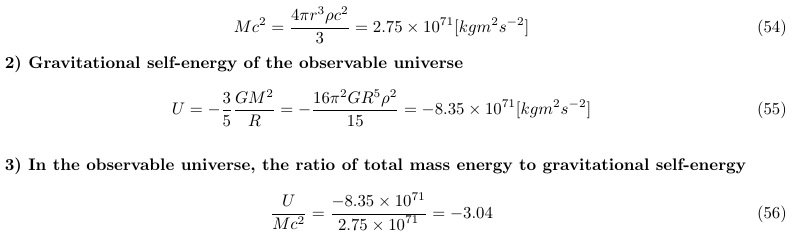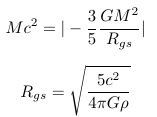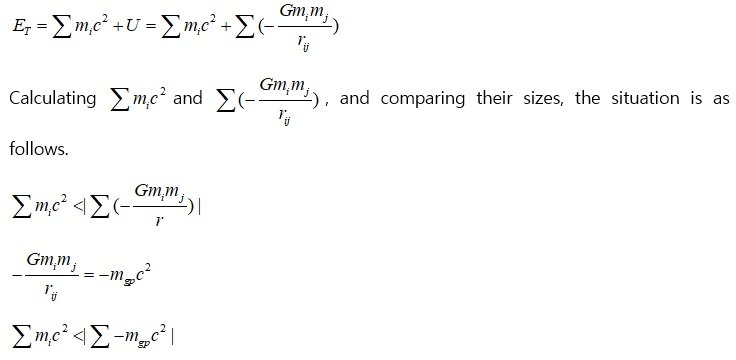icarus2
Registered Senior Member
The source of dark energy is gravitational self-energy or total gravitational potential energy!
1. The need for negative energy density
1) Negative energy (mass) density in standard cosmology
From the second Friedmann equation or acceleration equation,
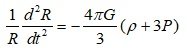
In standard cosmology, it is explained by introducing an entity that has a positive mass density but exerts a negative pressure.
ρ_Λ + 3P_Λ = ρ_Λ+3(-ρ_Λ) = - 2ρ_Λ
However, If we rearrange the dark energy term, the final result is a negative mass density of "- 2ρ_Λ" .
There are too many people who have an aversion to negative energy (mass). However, in the standard cosmology, accelerated expansion is impossible without negative mass density. It is just that the negative mass density term is called negative pressure, so it is not recognized.
2) The energy of a gravitational field is negative
In his lecture, Alan Guth said:
Stephen Hawking also argued that
3) Earth's and Moon's Gravitational self-energy
4) Mass defect due to binding energy

Consider situations a) and c)
In a), the total mass of the two particle system is 2m, and the total energy is E_T=2mc^2
In c), is the total energy of the two-particle system E_T=2mc^2 ?
In c), when the two particle system act gravitationally on an external particle, will they act gravitationally with a gravitational mass of " 2m "?
Are a) and c) the same mass or same state?
If you do not apply negative binding energy, the conclusions you get will not match the actual results.
In c), the total energy of the two particle systems is

In the dimension analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of mass x (speed)^2. So, E=mc^2 (Here, m is not used as a word for rest mass, but for mass.) holds true for all kinds of energy. If we introduce the equivalent mass -m_gp for the gravitational potential energy,
In the dimension analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of mass x (speed)^2. So, E=mc^2 (Here, m is not used as a word for rest mass.) holds true for all kinds of energy. If we introduce the equivalent mass -m_gp for the gravitational potential energy,


The gravitational force acting on a relatively distant third mass m3 is
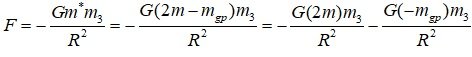
That is, when considering the gravitational action of a bound system, not only the mass in its free state but also the binding energy term should be considered. Alternatively, the gravitational force acting on the bound system can be decomposed into a free-state mass term and an equivalent mass term of binding energy.
While we usually use the mass m* of the bound system, we forget that m* is (m - m_binding-energy). Gravitational potential energy is also a kind of binding energy.
The same is true in cosmology. We have to consider not only mass energy, but also gravitational binding energy.
5) Our common sense was wrong long ago
Our conventional wisdom is already wrong about the accelerated expansion of the universe and the rotation curve of galaxies. So, instead of thinking about whether negative energy exists, we should focus on whether the universe is explained by the introduced physical quantity. For those of you who are still reluctant to negative energy, first assume that gravitational potential energy is negative energy, and then look at the following logic.
#On the solution of the strong gravitational field the solution of the Singularity problem the origin of Dark energy and Dark matter
https://www.researchgate.net/publication/359329109
1. The need for negative energy density
1) Negative energy (mass) density in standard cosmology
From the second Friedmann equation or acceleration equation,
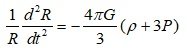
In standard cosmology, it is explained by introducing an entity that has a positive mass density but exerts a negative pressure.
ρ_Λ + 3P_Λ = ρ_Λ+3(-ρ_Λ) = - 2ρ_Λ
However, If we rearrange the dark energy term, the final result is a negative mass density of "- 2ρ_Λ" .
There are too many people who have an aversion to negative energy (mass). However, in the standard cosmology, accelerated expansion is impossible without negative mass density. It is just that the negative mass density term is called negative pressure, so it is not recognized.
2) The energy of a gravitational field is negative
In his lecture, Alan Guth said:
The energy of a gravitational field is negative! The positive energy
of the false vacuum was compensated by the negative energy of gravity.
Stephen Hawking also argued that
Zero energy state could be maintained when mass energy and gravitational potential energy were offset each other at the inflation period only.
3) Earth's and Moon's Gravitational self-energy
Treating the Earth as a continuous, classical mass distribution (with no gravitational self-energy in the elementary, subatomic particles), we find that its gravitational self-energy is about 4.6 x 10^-10 times its rest-mass energy. The gravitational self-energy of the Moon is smaller, only about 0.2 x 10^- 10 times its rest-mass energy. - GRAVITATION AND SPACETIME
4) Mass defect due to binding energy

Consider situations a) and c)
In a), the total mass of the two particle system is 2m, and the total energy is E_T=2mc^2
In c), is the total energy of the two-particle system E_T=2mc^2 ?
In c), when the two particle system act gravitationally on an external particle, will they act gravitationally with a gravitational mass of " 2m "?
Are a) and c) the same mass or same state?
If you do not apply negative binding energy, the conclusions you get will not match the actual results.
In c), the total energy of the two particle systems is

In the dimension analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of mass x (speed)^2. So, E=mc^2 (Here, m is not used as a word for rest mass, but for mass.) holds true for all kinds of energy. If we introduce the equivalent mass -m_gp for the gravitational potential energy,
In the dimension analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of mass x (speed)^2. So, E=mc^2 (Here, m is not used as a word for rest mass.) holds true for all kinds of energy. If we introduce the equivalent mass -m_gp for the gravitational potential energy,


The gravitational force acting on a relatively distant third mass m3 is
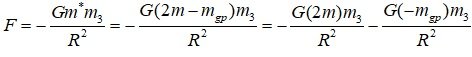
That is, when considering the gravitational action of a bound system, not only the mass in its free state but also the binding energy term should be considered. Alternatively, the gravitational force acting on the bound system can be decomposed into a free-state mass term and an equivalent mass term of binding energy.
While we usually use the mass m* of the bound system, we forget that m* is (m - m_binding-energy). Gravitational potential energy is also a kind of binding energy.
The same is true in cosmology. We have to consider not only mass energy, but also gravitational binding energy.
5) Our common sense was wrong long ago
Our conventional wisdom is already wrong about the accelerated expansion of the universe and the rotation curve of galaxies. So, instead of thinking about whether negative energy exists, we should focus on whether the universe is explained by the introduced physical quantity. For those of you who are still reluctant to negative energy, first assume that gravitational potential energy is negative energy, and then look at the following logic.
#On the solution of the strong gravitational field the solution of the Singularity problem the origin of Dark energy and Dark matter
https://www.researchgate.net/publication/359329109