You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
π/Φ Pi in the Phi
- Thread starter sly1
- Start date
Motor Daddy
Valued Senior Member
Yes. Do you agree that $$2\pi \times r = \pi \times 2r$$?
What is 2*pi?
You just don't like $$\pi$$ for being an irrational real number?
"The constant pi, denoted
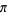 , is a real number defined as the ratio of a circle's circumference
, is a real number defined as the ratio of a circle's circumference
 to its diameter
to its diameter
 "
"
http://mathworld.wolfram.com/Pi.html
"The constant pi, denoted
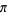


http://mathworld.wolfram.com/Pi.html
Yes, you got it, I think,So you're trying to figure out what the length of half of the circumference of a 10 meter diameter circle is? Well a 10 meter diameter circle has a circumference of 10*3.1416=31.416 meters. If you divide that by two, well there's your answer! You can find 1/360th of that circumference by dividing by 360, so 31.416/360=0.0872666666666667 meters. So each degree has a length of 0.0872666666666667 meters along the circumference of a 10 meter diameter circle.
29.385 degrees is a length of 29.385*0.0872666666666667=2.564331 meters along the circumference of a 10 meter diameter circle.
You can divide any circumference by 360
You can then divide Pi by 360
A division of the two gives the diameter.
1 degree =cir/360
1 degree=Pi/360
cir/Pi =2r or 1 di
t.s per rotation/360 = 1 degree
We could say Pi = 0.00872664625*360=PiYou just don't like $$\pi$$ for being an irrational real number?
"The constant pi, denoted, is a real number defined as the ratio of a circle's circumference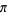 to its diameter
to its diameter "
"
http://mathworld.wolfram.com/Pi.html
69.0975850864/0.00872664625=7918.00000904
edit-sorry had to change value copied and pasted wrong one from my notes.
Last edited:
Motor Daddy
Valued Senior Member
You just don't like $$\pi$$ for being an irrational real number?
If 2*pi*r=pi*2*r, if you divide the left hand side and the right hand side by 2, they cancel and what you're left with is pi*r on both sides. pi*r=pi*r is what you're trying to prove?
But then we would be mathless slaves of a calculator and wrong. $$0.00872664625 = \frac{872664625}{10^{11}} = \frac{6981317}{8 \times 10^8}$$ so $$0.00872664625 \times 360 = \frac{62831853}{2 \times 10^7} =We could say Pi = 0.00872664625*360=Pi
3.14159265$$ which is a ratio of integers or a "rational number", and not equal to pi.
Two demonstrations with precision math that $$\pi \neq 3.14159265$$:
$$ \frac{62831853}{2 \times 10^7} + \frac{1}{ 278567576} \lt \pi \lt \frac{62831853}{2 \times 10^7} + \frac{1}{ 278567575} $$
$$ 278567576 \, \sin \left( \frac{62831853}{2 \times 10^7} \right) > 1$$ but $$ 278567576 \, \sin ( \pi ) = 0$$
By 69.0975850864 did you mean $$\frac{6909758508635}{10^{11}}$$, $$\frac{21179239}{306512}$$, $$\frac{690975850864}{10^{10}}$$, $$\frac{6909758508645}{10^{11}}$$, $$ \frac{3959 \pi}{180}$$, or $$\frac{24604199}{356079}$$ (which I have listed in ascending order)? How do you know? Does your source have that many digits of precision? Is this a physically measured quantity? What is the source?69.0975850864/0.00872664625=7918.00000904
Conventionally, a decimal quantity on a display with a fixed amount of display digits can stand for the whole range of numbers that round to that displayed number, so 69.0975850864 stands for all numbers, x, in the range $$\frac{6909758508635}{10^{11}} \leq x \lt \frac{6909758508645}{10^{11}}$$. But if you don't know which one, multiplication (on a calculator with only finite precision in operations) doesn't guarantee all the digits of your answer are exact.
But, garbage in leads to garbage out, so if you don't have a reason to know how accurate your source is, you can't know how accurate your answer is even if you do use arithmetic with absolute precision.
Last edited:
Motor Daddy
Valued Senior Member
circumference = diameter*pi (ratio of circumference to diameter (~3.1416:1)) = radius (1/2 of the diameter)*ri (ratio of circumference to radius (~6.2832:1))
How ya say...how do ya like them apples?
How ya say...how do ya like them apples?
Last edited:
1+1 = 2 and 2+2=4 and dividing both sides of that equation by 2 we get 1+1=2!
Radius, circumference and diameter are not defined numbers like $$\pi$$ Otherwise, all circles would be the same size.
Radius, circumference and diameter are not defined numbers like $$\pi$$ Otherwise, all circles would be the same size.
Motor Daddy
Valued Senior Member
1+1 = 2 and 2+2=4 and dividing both sides of that equation by 2 we get 1+1=2!
Radius, circumference and diameter are not defined numbers like $$\pi$$ Otherwise, all circles would be the same size.
There is a unit of measure of distance called the meter. It is defined as the length of the path that light travels in 1/299,792,458 of a second in a vacuum.
If a light sphere is emitted at t=0 it has a radius of 1 meter and a diameter of 2 meters at t=1/299,792,458 of a second.
Agreed?
Last edited:
Mathematics uses abstraction and you want to use physical things that are not.
Agreeing with or not would be irrelevant.
Agreeing with or not would be irrelevant.
Motor Daddy
Valued Senior Member
Mathematics uses abstraction and you want to use physical things that are not.
Agreeing with or not would be irrelevant.
So just clarify for me, then, what is 2pi?
2 x a mathematical constant.
Motor Daddy
Valued Senior Member
2 x a mathematical constant.
That constant is a constant RATIO, like the gear ratio in the rear end of your car. If a gear ratio is 3.1416:1, that means that 3.1416 turns of the input shaft is equal to 1 turn of the output shaft. If the tire has a diameter of... and the rpm is... oh you do the math!
The point is, you're wrong!
I did post this earlier:
Spheres and cylinders are not constant. So how can I be wrong? They all use the same mathematical constant as $$\pi$$, but not the others.
Radius, circumference and diameter are not defined numbers like $$\pi$$ Otherwise, all circles would be the same size.
Spheres and cylinders are not constant. So how can I be wrong? They all use the same mathematical constant as $$\pi$$, but not the others.
Motor Daddy
Valued Senior Member
I did post this earlier:
Spheres and cylinders are not constant. So how can I be wrong?
So you measure variable spheres and cylinders? Do they change colors too?

But then we would be mathless slaves of a calculator and wrong. $$0.00872664625 = \frac{872664625}{10^{11}} = \frac{6981317}{8 \times 10^8}$$ so $$0.00872664625 \times 360 = \frac{62831853}{2 \times 10^7} =
3.14159265$$ which is a ratio of integers or a "rational number", and not equal to pi.
Two demonstrations with precision math that $$\pi \neq 3.14159265$$:
$$ \frac{62831853}{2 \times 10^7} + \frac{1}{ 278567576} \lt \pi \lt \frac{62831853}{2 \times 10^7} + \frac{1}{ 278567575} $$
$$ 278567576 \, \sin \left( \frac{62831853}{2 \times 10^7} \right) > 1$$ but $$ 278567576 \, \sin ( \pi ) = 0$$
By 69.0975850864 did you mean $$\frac{6909758508635}{10^{11}}$$, $$\frac{21179239}{306512}$$, $$\frac{690975850864}{10^{10}}$$, $$\frac{6909758508645}{10^{11}}$$, $$ \frac{3959 \pi}{180}$$, or $$\frac{24604199}{356079}$$ (which I have listed in ascending order)? How do you know? Does your source have that many digits of precision? Is this a physically measured quantity? What is the source?
Conventionally, a decimal quantity on a display with a fixed amount of display digits can stand for the whole range of numbers that round to that displayed number, so 69.0975850864 stands for all numbers, x, in the range $$\frac{6909758508635}{10^{11}} \leq x \lt \frac{6909758508645}{10^{11}}$$. But if you don't know which one, multiplication (on a calculator with only finite precision in operations) doesn't guarantee all the digits of your answer are exact.
But, garbage in leads to garbage out, so if you don't have a reason to know how accurate your source is, you can't know how accurate your answer is even if you do use arithmetic with absolute precision.
Pffff, I got the 69 number from a circumference divided by 360.
Your maths is far to advanced for me, I do not have a clue what all your numbers mean.
So you measure variable spheres and cylinders? Do they change colors too?
$$V=\frac{4 \text{$\pi $r}^3}{3},A=4 \text{$\pi $r}^2,\text{and } V=h \text{$\pi $r}^2$$
Can you point out the variables in those equations?
Motor Daddy
Valued Senior Member
$$V=\frac{4 \text{$\pi $r}^3}{3},A=4 \text{$\pi $r}^2,\text{and } V=h \text{$\pi $r}^2$$
Can you point out the variables in those equations?
Trying to avoid how you explain how you measure a changing cylinder's diameter and circumference??
You said, "Spheres and cylinders are not constant."
So you're trying to say the cylinder is changing?
Why don't you just be quiet and think for once.
