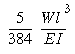Calculating the value of Deflection

[Eagle9]

Here we have got tall skyscraper and long cylindrical rod placed on it and on the land (the angle between rod and skyscraper is equal to 45 degrees). If we know rod’s properties (length, mass, thickness) and parameters of the material that was used for manufacturing the rod (its density, Young’s modulus, specific strength an etc) then how can we calculate the value of Deflection? Is there any formula for this purpose? I think that this calculator can help me
And-when we calculate the value of deflection can we decide if the rod breaks or not? If this value is too high then the rod will be bent and perhaps will be broken

 

[Pinwheel]

The deflection will be due to the mass of the rod. As its at 45deg then there will be a component of the load in the axial direction (along the beam) and a component at 90deg to the beam (the direction of the deflection you have drawn). I guess you can ignore the axial component if the beam is fixed at both ends in translational degrees of freedom only (ie no axial flexibility). So you can try that formula you've linked to where the uniformly distributed load is the load per unit length along the beam based on its density and area.

 

[Eagle9]

Pinwheel

The deflection will be due to the mass of the rod. As its at 45deg then there will be a component of the load in the axial direction (along the beam) and a component at 90deg to the beam (the direction of the deflection you have drawn). I guess you can ignore the axial component if the beam is fixed at both ends in translational degrees of freedom only (ie no axial flexibility).

So you can try that formula you've linked to where the uniformly distributed load is the load per unit length along the beam based on its density and area.

Well, I will try to calculate and then you tell me if I am right
Length of beam, L-Let it be 1 000 meters.
Line pressure load on beam, p: as I know in my case it will simply be the weight per meter length. So, if my rod’s radius is 1 meter then the volume of rod’s this part would be 3.14 m^3. As for its mass, if I use Carbon nanotubes their density varies between these values: 0.037-1.34 g/cm^3 (http://en.wikipedia.org/wiki/Specific_strength). Let’s take some medium value-0.1 g/cm^3, so the mass of that part will be 314 kg. But how can I transform this value to Pa-m?
Young's Modulus, E: for Carbon nanotubes is equal to 1 000 GPa, or 10^12 Pa http://en.wikipedia.org/wiki/Young's_modulus
Distance from neutral axis
to extreme fibers-as I know this will be the radius of the rod-1 meter
Moment of Inertia, I: it is equal to (pi*r^4)/4, so it is equal to 0.785

But my rod is inclined by 45 degrees, what should I do with this circumstance? Nothing? Just ignore it?

 

[arfa brane]

But my rod is inclined by 45 degrees, what should I do with this circumstance?

I would be thinking about what happens to a flexible cable (or rod) when it's hanging between two fixed points. Then what happens if the material is less flexible so it can "restore" some of its original shape against the downward force of gravity instead of deforming passively, say like a chain or a rope does.

The calculator you're using doesn't seem to have a way to analyse beams that aren't level; I'd look for one that does or use the "right" formula for a flexible beam that has its ends at different heights. But have a look at the hanging cable problem and maybe use that as a starting point.

 

[Pinwheel]

But my rod is inclined by 45 degrees, what should I do with this circumstance? Nothing? Just ignore it?

No you dont ignore it. If you just ignore the axial component as I said, then you just factor your line load by cos(45) = 0.7071. Ie instead of 100% load you use 70%.

 

[Pinwheel]

Line pressure load on beam, p: as I know in my case it will simply be the weight per meter length. So, if my rod’s radius is 1 meter then the volume of rod’s this part would be 3.14 m^3. As for its mass, if I use Carbon nanotubes their density varies between these values: 0.037-1.34 g/cm^3 (http://en.wikipedia.org/wiki/Specific_strength). Let’s take some medium value-0.1 g/cm^3, so the mass of that part will be 314 kg. But how can I transform this value to Pa-m?

I would cheat and use the drop down to change the units to N/m.

Then take line load in N/m to be density*area*g =~3080N/m which you then factor by cos(45) =~2180N/m

 

[Eagle9]

arfa brane

I would be thinking about what happens to a flexible cable (or rod) when it's hanging between two fixed points. Then what happens if the material is less flexible so it can "restore" some of its original shape against the downward force of gravity instead of deforming passively, say like a chain or a rope does.
But have a look at the hanging cable problem and maybe use that as a starting point.

As far as I know the way for calculating the deflection for ropes is different and if I still calculate the deflection it will be quite difficult to “restore” the original situation for rod…..have you ever tried this?

I'd look for one that does or use the "right" formula for a flexible beam that has its ends at different heights.

Great but is there anywhere such formula?

Pinwheel

No you dont ignore it. If you just ignore the axial component as I said, then you just factor your line load by cos(45) = 0.7071. Ie instead of 100% load you use 70%.

would cheat and use the drop down to change the units to N/m.
Then take line load in N/m to be density*area*g =~3080N/m which you then factor by cos(45) =~2180N/m

Yes………100 (kg/m^3)*3.14^2 (area of rod’s cross-section I square meters)*9.8 (m/sec^2)*0.7=~2180N/m I received almost the same result So, I should use this value 2180 and change unit to N/m, right?

Then what? What should I do now?

 

[Pinwheel]

Then what? What should I do now?

Sit back, have a cigar? Do what you want, what was the purpose of the calculation? If you want to know if the bar will bend permanently you can compare the stress at the extreme fibre with the material yield stress. You can use the ultimate stress for the material for the stress at which it breaks.

 

[Eagle9]

Pinwheel

Sit back, have a cigar? Do what you want, what was the purpose of the calculation?

I need to find the value of deflection

If you want to know if the bar will bend permanently you can compare the stress at the extreme fiber with the material yield stress.

You can use the ultimate stress for the material for the stress at which it breaks.

And where is it possible to find these values?

 

[Pinwheel]

I need to find the value of deflection

Then click on Displacement. :m:

 

[Eagle9]

Pinwheel

Then click on Displacement

I did so and I received minus 36.2 m value, is this value of deflection?

Or something else is needed to do and to calculate?

 

[Pinwheel]

Yeah. That seems high but then again, your "beam" is 1km long!!

 

[Eagle9]

Pinwheel

Yeah. That seems high but then again, your "beam" is 1km long!!

So, the deflection value will be 36.2 m downwards….
Now, how can I check if this rod will be broken or not?

Actually I tried to use this online-calculator http://www.engineersedge.com/beam_bending/calculators_protected/beam_deflection_1.htm and put the same values, however the result that appeared there are different from that 36 meters, so this calculator is useless?

There is nothing written about that angle-45 degrees

 

[Pinwheel]

I think you need to check your units, you're mixing psi with m with lbs etc. An none of these calculators have the 45 angle becasue they all assume horizontal beams. It doesnt matter in this case as long as you adjust the load as we did in the first example.

 

[Eagle9]

Pinwheel

I think you need to check your units, you're mixing psi with m with lbs etc.

Yes, I think that you are right, in Modulus of Elasticity (E) I should have written 1000 GPa for Carbon nanotubes (value taken from here: http://en.wikipedia.org/wiki/Young's_modulus) and not 145 million psi, but the point is that for other fields I chose the metric values while this field Modulus of Elasticity (E) receives only imperial value-psi:

An none of these calculators have the 45 angle becasue they all assume horizontal beams. It doesnt matter in this case as long as you adjust the load as we did in the first example.

You mean your post N 6?:

Then take line load in N/m to be density*area*g =~3080N/m which you then factor by cos(45) =~2180N/m

You adjusted all other values (area’s cross-section, material’s density and gravity) under angle- cos(45), right?

 

[Pinwheel]

this field Modulus of Elasticity (E) receives only imperial value-psi:

You can use whatever units you like as long as you're consistent. It tells you that on the webpage itself:
http://www.engineersedge.com/beam_bending/beam_bending1.htm
If you are working in N and m, you need to use Pa (=N/m^2).

You should get the same answer because the equation is :

which is effectively the same as the equation on the first calculator, except instead of line load per m it uses total load, W. They both do the same thing. W = density x area x length x g.

You adjusted all other values (area’s cross-section, material’s density and gravity) under angle- cos(45), right?

I dont understand what you're saying here. I only multiplied the product of density, area and g by (cos 45).

 

[Eagle9]

Pinwheel

You can use whatever units you like as long as you're consistent. It tells you that on the webpage itself:
http://www.engineersedge.com/beam_bending/beam_bending1.htm
If you are working in N and m, you need to use Pa (=N/m^2).

You should get the same answer because the equation is :

which is effectively the same as the equation on the first calculator, except instead of line load per m it uses total load, W. They both do the same thing. W = density x area x length x g.

Well, if so I will use only that first calculator that I posted in my first post and then do to Displacement since exactly this value is the value of deflection that I am seeking as for that formula:

it makes one problem since at that site the Modulus of Elasticity needs to be indicated in N/m^2 while the values of Young's modulus at this site http://en.wikipedia.org/wiki/Young's_modulus are shown in GPa, so additional conversion is needed.....

 

[Eagle9]

Well, as I see you wrote one billion in Modulus of Elasticity psi (E) field, this is exactly 1 000 GPa that is indicated in Wikipedia for Carbon nanotubes

I dont understand what you're saying here. I only multiplied the product of density, area and g by (cos 45).

Yes, I will multiply area*density*g*COS45 and write the result in Line pressure load on beam, p: field (I will choose N/M from menu) and after calculation I will go to Displacement and that will be value of deflection, everything is right?

 

[Pinwheel]

Well 1 Pa is defined as 1 N/m^2. GPa is just Giga Pascals, ie 1,000,000,000 Pa.

 

[Eagle9]

Pinwheel

Well 1 Pa is defined as 1 N/m^2. GPa is just Giga Pascals, ie 1,000,000,000 Pa

Well, I did not know this, thanks
I will try to calculate now myself:
With this calculator:

The result is the same: Maximum Deflection at Center (y) =35.48177 meters
But I would like to clarify two things:
What should be written in Distance to neutral axis/plane (Z)? You wrote 1000, I wrote the same 1000 and then changed to 1, but the result in Maximum Deflection at Center (y) remained the same, but still perhaps it is better to write there 1-this is the radius of rod's cross-section
You wrote 500 in Distance (x), may I know why? This is half of rod's length. I tested there various values but the result in Maximum Deflection at Center (y) stayed the same again....