(continued...)
I'll try to explain. A mountain lake has the potential to be used as a power source for electricity. The water in that lake provides the potential for such a conversion, but as long as the water is contained this potential is a latency. Now we build a pipe from the lake down the mountain to let the water flow down and acquire a kinetic force which drives a generator to produce electricity. Now the potential of the water as a source for generating power has been realized?
You didn't answer the question I asked you, which was: how can a non-physical "potential" create physical things?
In your hydroelectric example, the lake's "potential" to be used as a power source doesn't create the pipe or the generator. People do that. That "potential" on its own does nothing.
Your argument, you will recall, is that the entire universe came about because a non-physical "potential" somehow created everything out of nothing. But how?
I disagree with the assumption that time for an event has to exist before an event occurs. IMO, time is an emergent property of duration and is a measurement only of the duration of that specific event. The production (emergence) of time is a simultaneous result of duration.
Okay, so you have an opinion. Based on what?
Tell me, in detail, how time emerges from "duration". What does that even mean? Does it mean anything, in fact, or is it just words?
This might fit Krauss' perspective of something emerging from nothing?
I don't think anything Krauss has written is remotely like what you just claimed.
We have spacetime because the universe is dynamic.
How does the universe's dynamicism create spacetime? Explain.
A massive Black Hole of unimaginable density and mass? We know mass does warp (bend) spacetime toward its center. i.e mass has influence over spacetime. Perhaps sufficient mass might actually swallow spacetime along with everything else?
Spacetime is the background against which events occur. It isn't a thing that can be swallowed. The bending of spacetime is a metaphor, or a model if you prefer. We describe it that way because the mathematics of gravity turns out to be closely related the mathematics of curved surfaces.
Just as time is an emergent measurement, Pi can be derived at (emerges) from dropping a needle multiple times on a flat surface that has straight lines (spaced by the length of the needle). This is a proven fact according to Mario Livio.
You're referring to a measurement of the probability of a dropped needle falling randomly across a line. Dropping a needle doesn't
cause the number pi. It just happens that the relevant probability calculation involves the number pi in the result. The reason for that, I think, has something to do with the fact that the needle has a random orientation when it lands - i.e. it has rotation, and as we know pi is related to circles. In other words, in a sense pi was "built into" the experiment from the start.
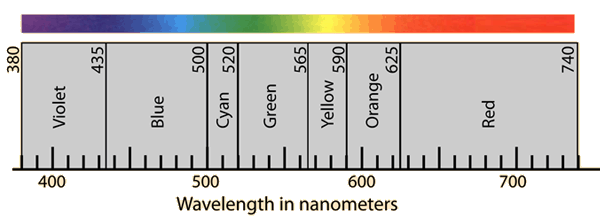
The number of the wave frequency determines the appearance of a color, just as the frequency of a sound wave determines the pitch.
There's a separate discussion going on about this in a different thread. For present purposes, it is enough to say that the numerical value of the wavelength of a certain type of light is a measurement of a quantity (wavelength), not of a quality (color).
I have to qualify your question that a potential is a "thing", I see "potential" as a latency with a mathematical value, that may become reality.
Part of the problem I'm having is that you are inconsistent with the way you are using words like "potential". For example, just above, you said "A mountain lake has the potential to be used as a power source for electricity." So, am I to take it you meant "A mountain lake has a latency with a mathematical value to be used as a power source for electricity"?
Is the type of "latency" you refer to the same in every example, or does it change with the example?
Can you please be more specific about the particular thing that is latent with a mathematical value in the mountain lake? Is that the same thing that was latent in the big bang, or is it something different?
You say:
How that may be measured depends on the thing that contains the latent potential. (see my example of the lake above)
So it seems that your "potential" varies along with the particular situation. What is the use of the word "potential", if its meaning is different for every example?
I have struggled with that for some time now. IMO, it is both. Using fractals a map can represent the terrain accurately down to Planck scale.
You took what I wrote literally rather than figuratively. Haven't you heard that saying before?
The point is: the description of a thing is not the thing itself. For instance, you quoted with approval the idea that "color is the frequency of light". But color isn't a frequency of light. The frequency of light is a number we assign when we take a particular kind of measurement. Color is a physical property that we perceive with our eyes. We find, of course, that the frequency of light is
correlated with the color we observe, but it is a mistake to imagine that the frequency therefore
is the color, or vice versa.
James R said:
Pi is defined to be a specific number. It has only one value, neither infinitely large nor infinitely small. It's approximately 3.14159.
Write4U said:
Pi is an irrational number and has no specific value into infinity (as far as I know)
Wrong. pi is a number that has a specific value. It is theoretically possible to calculate the exact value to as many decimal places as you require. It couldn't be any more specific than that.
Recall your original claim: "Pi is an irrational number which can be infinitely large or infinitely small."
Pi is an irrational number. The term "irrational number" has a precise technical meaning in mathematics; it doesn't mean that pi is crazy or follows no rules or anything like that. It is certainly
not infinitely large or infinitely small. It is finite. It's value is close to 3, which is neither infinitely large nor infinitely small.
Please tell me we are on the same page about pi, after all this. If you can't get a simple piece of mathematics like this straight, then everything else is bound to be an almost insurmountable battle.
no I am not, scientists are. I believe it's called physics.
The term "potential" is well defined in physics (it is related to energy). It is not used in the sense you have been using it. "Mathematical latency" is not a term I have ever come across in physics.
Give me a non-mathematical equation of a universal constant that can be used in any calculation.
What on earth would a
non-mathematical equation look like? Please give me an example so I know what you're talking about.
The Higgs boson was mathematically (not physically) predicted.
The Higgs boson was the prediction of a mathematical, physical theory. Its existence was hypothesised in an attempt to solve an unsolved problem in particle physics. The theory was testable in that it predicted the existence of a particular particle with particular properties. It was tested in the Large Hadron Collider and found to be consistent with observations made there - i.e. the LHC found the predicted particle.
Mathematical values and functions (patterns) are the informational language of universal phenomena. he universe is essentially mathemayical. Physics is the symbolic descriptive language of humans we assigned to mathematical values and functions of universal mathemaytical patterns.
The ongoing problem I'm having with you here is that you seem to believe not merely that mathematics is useful for
describing the universe, but that the universe
is mathematics. In doing that, you're again mistaking the map for the territory. By that I mean that mathematics is used as a tool to build testable physical models of the universe. But you appear to think that those models
are the universe, or that the universe
is the models.
It's equivalent to saying that 17 lb is a rock.


:max_bytes(150000):strip_icc():format(webp)/kinetochore-56a09b673df78cafdaa32fb4.jpg)