Write4U
Valued Senior Member
What is a "temporal plane"?
How many dimensions can a temporal plane have?
Do temporal planes of dimensions other than 2 have the same NOW?
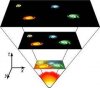 Chronologically stacked 2D temporal planes.
Chronologically stacked 2D temporal planes.No I didn't. If anything I said "temporal planes" and the chronology of universal NOW is measured in 2D slices (planes) of time. In the illustration "x" and "y" compromise 1 "horizonal " spatial plane of NOW, "t" is the vertical temporal stacking of the horizontal spatial NOWS.Temporal dimensions, plural, you mean. You said it is a 2 dimensional temporal plane, remember?
You introduced the "thought experiment" of placing "observers" (alarm clocks) in relative positions on the horizontal spatial plane, no?How can an alarm clock - a physical object - be placed on a temporal plane? Wouldn't there need to be some spatial dimensions for the alarm clock to exist in, and not just temporal ones?
The plot thickens!
No no, you can't get away with that.Why does the introduction of an observer introduce a spatial dimension? Just one spatial dimension, or more than one? It sounds like just one, because you mention "3D relativity". So, two temporal dimensions and 1 spatial dimension?
The present consists of a single horizontal slice of spatial (physical) existence on the vertically stacked slices of NOWs
Your introduction of the physical "past" to the equation of the "present NOW".What is "3D relativity"?
Because the "present" is not a 3D object. There is no temporal "past present" except when you introduce a spatial observer. Then you get a spatial past present experienced only by the observer. Remove the observer and there is only NOW.And how does this 2 time, 1 space universe relate to our own 1 time, 3 space universe?
That is your argument, not mine.Is this just an overly-complicated way of saying that sound takes time to travel from place to place?
But the doppler effect is a good way to illustrate it.
======================(train travelling -->)===================
Observer A<_ _ _ _ _ _ _ [------- Sound source -------] .............> Observer B
Both observers get a subjectively false experience of the true pitch of the sound. And so it is with time.
IOW time has an objective NOW . Observers experience a subjective relative NOW depending on their POV.
It is only real to the observer and not necessarily to the whole. It is relative to the POV.What's a "subjective relative reality"? What is it relative to? How is it real?
That is all you have been talking about.What does "differential sychronization" of clocks mean?
Compensate for the relativity introduced with the POV of an individual observer (each clock is adjusted to compensate for time lag SOL over long distances of observation). That is a subjective approach. Objectively there is no time lag over the entirety of the present spatial plane.What does it mean to "mediate" a subjectively relative reality?
I think I addressed all those questions.On your 2 dimensional temporal plane, you mean?
What is "temporal synchronicity"?
What does "objective" mean, in this context?
How does an observerless 2 dimensional temporal plane relate to our 1 time, 3 space universe in which there are observers?
I am glad you admitted to the introduction of physical observers in the analysis of a temporal dimension, which introduces a differential equation.
The thing is that your description admits there is no such thing as Time at all, but is merely a subjective experience of observational phenomena.
Actually I agree with that. I believe time is an emergent property of duration of a chronological event in a timeless permittive nothingness. So you can assign a time frame (timeline) to everything that has an observable duration.
Question: does time exist without an observer? Can the Universe be its own observer and experience its own NOW?
Last edited:

