DaveC426913
Valued Senior Member
I was snacking on some Hallowe'en "Fun size" smarties, and noticed this symbol on the box lid (I presume it is a some visual calibration glyph for automated assembly systems):

I thought it was interestingly geometric so I thought I'd deconstruct it. This is what I got:

So now I'm trying to figure out what ratio that second smaller square is to the full-sized square. It's self-referential:

I took me a while to realize that this is an example of the Golden Ratio.
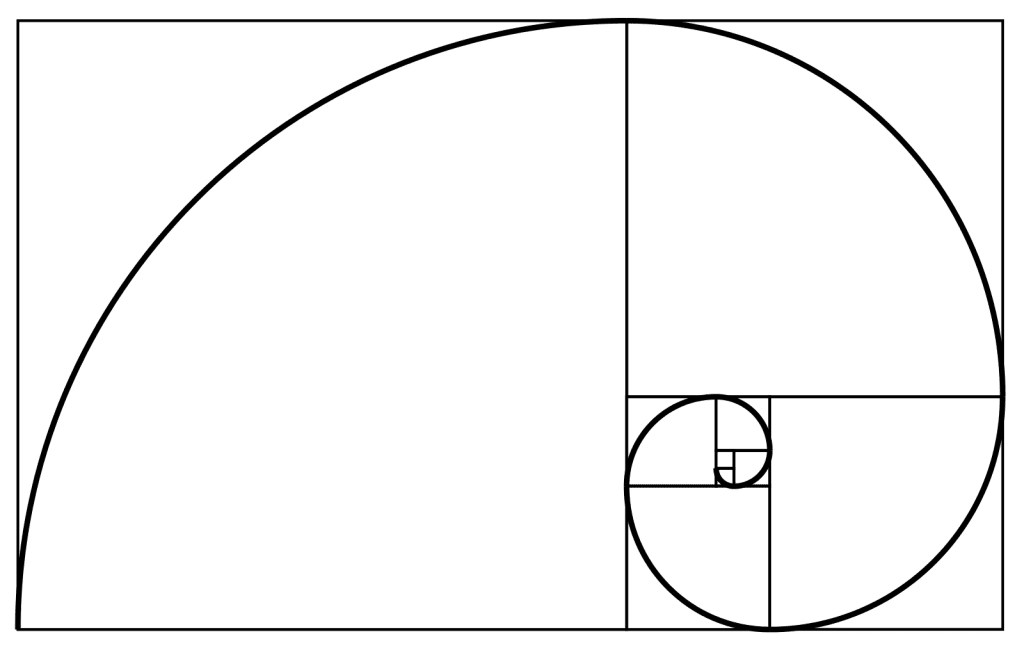
You can see it here, where the length of square 3 equals the sum of square 2 and square 1. And it doesn't matter which squares you choose:

How big is a large square as a ratio of a smaller square? ~1.618:1 - the Golden Ratio.
What's even more cool is the correlation with the Fibonacci Series.
When I measured the lengths of the squares in pixels, I got the following:
2, 3, 5, 8, 13, 21, 34, 55
i.e. the Fibonacci Series itself. Any given number is the sum of the previous two numbers, no matter which number you start at.
What is the ratio of any two adjacent numbers in the Fibonacci Series? ~1.618.
I wonder if that symbol has a special meaning in this context.

I thought it was interestingly geometric so I thought I'd deconstruct it. This is what I got:

So now I'm trying to figure out what ratio that second smaller square is to the full-sized square. It's self-referential:

I took me a while to realize that this is an example of the Golden Ratio.

You can see it here, where the length of square 3 equals the sum of square 2 and square 1. And it doesn't matter which squares you choose:

How big is a large square as a ratio of a smaller square? ~1.618:1 - the Golden Ratio.
What's even more cool is the correlation with the Fibonacci Series.
When I measured the lengths of the squares in pixels, I got the following:
2, 3, 5, 8, 13, 21, 34, 55
i.e. the Fibonacci Series itself. Any given number is the sum of the previous two numbers, no matter which number you start at.
What is the ratio of any two adjacent numbers in the Fibonacci Series? ~1.618.
I wonder if that symbol has a special meaning in this context.
