Pinball1970
Valued Senior Member
If this continues much longer with phyti and River I am going to rename you, "Canadian Dave who is patient, called Dave the patient."
The Monty Hall Problem Revisited
- Thread starter raydpratt
- Start date
It's pointless trying to explain their error to this person, as they are profoundly deaf to it.
8 possible outcomes, sure: 2 for game 1, 2 for game 2, and 4 for game 3. But each game has equal probability, not each outcome. So the 4 outcomes for game 3 are each half as likely as the 2 outcomes for games 1 and 2. I know that. You know that. Anyone who understands the Monty Hall problem knows that. Phyti doesn't. And is seemingly unwilling to listen to explanations, rather just repeating their fallacious reasoning. Or they are unable to comprehend. Either way: pointless to try to explain any further.
DaveC426913
Valued Senior Member
I'd be happy if he just looked at the data. Data speaks for itself, and trumps theory.
And this data is way easier to analyze to find fault. All he has to do is find a row (or column) that violates any of the principles. The error will be self-explanatory and will be immediately obvious to all.
Which, I strongly suspect, is the very reason why he is silent about it. Because he has nada to refute it.
DaveC426913
Valued Senior Member
I am conscientiously taking my cue from James, who manages to find a way to ask insightful questions where I would otherwise just mock.
phyti:
Last time.
Here are all possible games, with the probabilities that the player will end up playing each variant, if he chooses randomly between the "switch" and "stay" options when given the chance to switch doors. Again, the assumption here is that the car is behind door c.
So, for instance, the notation "bac" means "Player initially chooses door b; host opens door a; door c is the last door to be opened".
There are four variants for "stay" and four for "switch".
The player wins with the "stay" strategy in games 5 and 7, only.
Total probability that player wins given that he chooses "stay" = (1/12+1/12) / (1/6+1/6+1/12+1/12)=(1/6) / (1/2)=1/3
The player wins with "switch" strategy in games 2 and 4, only.
Total probability that the player wins given that he chooses "switch" = (1/6 + 1/6) / (1/6 + 1/6 + 1/12 + 1/12) = (1/3) / (1/2) = 2/3
=====
More explanation, since you're (uncharacteristically) struggling with the maths:
Consider, for instance, game 3. The probability that the player initially chooses door b is 1/3. In that case, the probability that the host opens door a is 1, because the host cannot open the door the player chose and he cannot open the door with the car. The player then has a 1/2 of choosing to "stay". So, total probability for game 3 is 1/3 times 1 times 1/2 = 1/6.
Compare to a game where the player initially chooses the car. For example, game 8. The probability that the player initially chooses door c is 1/3. The probability that the host then chooses to open door b is 1/2 (because the host could have chosen door a instead, in this case). Then, the player has a 1/2 chance of choosing "switch". So, total probability of game 8 is 1/3 times 1/2 times 1/2 = 1/12.
===
Do you accept this analysis, phyti?
Last time.
Here are all possible games, with the probabilities that the player will end up playing each variant, if he chooses randomly between the "switch" and "stay" options when given the chance to switch doors. Again, the assumption here is that the car is behind door c.
So, for instance, the notation "bac" means "Player initially chooses door b; host opens door a; door c is the last door to be opened".
Code:
Game Order Outcome Player strategy Probability of playing this game
1 abc Loss Stay 1/6
2 abc Win Switch 1/6
3 bac Loss Stay 1/6
4 bac Win Switch 1/6
5 cab Win Stay 1/12
6 cab Loss Switch 1/12
7 cba Win Stay 1/12
8 cba Loss Switch 1/12There are four variants for "stay" and four for "switch".
The player wins with the "stay" strategy in games 5 and 7, only.
Total probability that player wins given that he chooses "stay" = (1/12+1/12) / (1/6+1/6+1/12+1/12)=(1/6) / (1/2)=1/3
The player wins with "switch" strategy in games 2 and 4, only.
Total probability that the player wins given that he chooses "switch" = (1/6 + 1/6) / (1/6 + 1/6 + 1/12 + 1/12) = (1/3) / (1/2) = 2/3
=====
More explanation, since you're (uncharacteristically) struggling with the maths:
Consider, for instance, game 3. The probability that the player initially chooses door b is 1/3. In that case, the probability that the host opens door a is 1, because the host cannot open the door the player chose and he cannot open the door with the car. The player then has a 1/2 of choosing to "stay". So, total probability for game 3 is 1/3 times 1 times 1/2 = 1/6.
Compare to a game where the player initially chooses the car. For example, game 8. The probability that the player initially chooses door c is 1/3. The probability that the host then chooses to open door b is 1/2 (because the host could have chosen door a instead, in this case). Then, the player has a 1/2 chance of choosing "switch". So, total probability of game 8 is 1/3 times 1/2 times 1/2 = 1/12.
===
Do you accept this analysis, phyti?
gmilam;
post 110
"Assume contestant selects door 1"
Then that event is a certainty, probability=1.
The host's choices determine the last door.
Using your table
The 1st 4 games resulted in a car. That's 50% of games.
The 2nd 4 games resulted in a goat. That's 50% of games.
Looks like no difference to stay or switch.
post 110
"Assume contestant selects door 1"
Then that event is a certainty, probability=1.
The host's choices determine the last door.
Using your table
The 1st 4 games resulted in a car. That's 50% of games.
The 2nd 4 games resulted in a goat. That's 50% of games.
Looks like no difference to stay or switch.
sarkus;
post 115
The possibility of winning a prize is represented in the 3 tree graphs.
The probability is 1/3 before the player's 1st choice, but 1 after the choice.
What follows are all possible choices resulting from the hosts action,
which excludes opening a door containing a car.
Column p is players 1st choice
Column h are host choices.
If h is possible then op is the prize behind the remaining closed door.
There are 4 results.
The player wins a car only if it is not behind his 1st choice, which is 50%.
The left tree is the general game, the right tree has the goat substitution.
post 115
The possibility of winning a prize is represented in the 3 tree graphs.
The probability is 1/3 before the player's 1st choice, but 1 after the choice.
What follows are all possible choices resulting from the hosts action,
which excludes opening a door containing a car.
Column p is players 1st choice
Column h are host choices.
If h is possible then op is the prize behind the remaining closed door.
There are 4 results.
The player wins a car only if it is not behind his 1st choice, which is 50%.
The left tree is the general game, the right tree has the goat substitution.
JamesR;
This example would result in switching wins 4 of 6 times, but
this example is not all possible games. It is the same distribution of prizes played in 2 games, for the player in each door. What you need is all possible 6 distributions for 1 door. That will be the same for the other 2 doors.
The stay vs switch is done by comparing player door with op door.
This example would result in switching wins 4 of 6 times, but
this example is not all possible games. It is the same distribution of prizes played in 2 games, for the player in each door. What you need is all possible 6 distributions for 1 door. That will be the same for the other 2 doors.
The stay vs switch is done by comparing player door with op door.
DaveC426913
Valued Senior Member
Reported as continuing to ignore the data.
DaveC426913
Valued Senior Member
Reported as continuing to ignore the data.
DaveC426913
Valued Senior Member
Reported as continuing to ignore the data.
My conclusion is that you are a troll.
My conclusion is that you are stupid.
DaveC426913
Valued Senior Member
My conclusion is that you are wilfully turning your back on what the actual circumstance shows to be the case.
There's a term for phyti's behviour if this thread: it's called sealioning.
"Sealioning is a form of online trolling where someone relentlessly pursues others with questions and requests for evidence*, often about previously addressed topics or seemingly unrelated points, while maintaining a pretense of civility and sincerity..."
* or presenting their own evidence relentlessly, with zero regard for continued challenges to it.
There's a term for phyti's behviour if this thread: it's called sealioning.
"Sealioning is a form of online trolling where someone relentlessly pursues others with questions and requests for evidence*, often about previously addressed topics or seemingly unrelated points, while maintaining a pretense of civility and sincerity..."
* or presenting their own evidence relentlessly, with zero regard for continued challenges to it.
DaveC;
Using your data, I showed game 1 as a composite of game1a and 1b. You did what Savant did, consider g1 and g2 as a generic g. The host can’t switch from opening door2 to opening door3 using 1 game. Each game has the same 3 events including host opens doorx. Game 1 would also produce a bias in the data, resulting in different frequencies for some games.
Using your data, I showed game 1 as a composite of game1a and 1b. You did what Savant did, consider g1 and g2 as a generic g. The host can’t switch from opening door2 to opening door3 using 1 game. Each game has the same 3 events including host opens doorx. Game 1 would also produce a bias in the data, resulting in different frequencies for some games.
JamesR;
Too confusing when door is c and car is c, and player chooses different doors.
Your effort is to reproduce Savant's explanation.
Mine is to show errors in Savant's explanation.
That is done with a complete list of games for 1 door, playing each one by the rules, then comparing door1 with the OPtional door for any advantage.
It does not require any probabilities or repetitions of games.
Who adds 2+3 100 times to prove the result is 5?
A quote from her 1990 original answer (about age 45).
"Yes; you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened. Suppose there are a million doors, and you pick door #1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?"
Naive or lack of experience or both! She believes the probability of each door to literally be 1/M, and as the doors are opened revealing no car, their contribution is transferred to the remaining doors, finally to #777,777, but not to the door containing the car!
Just another reason for my personal philosophy,
'There are no experts, only some people with more experience than others'.
Those 1000's who disagreed with her are on my side.
Too confusing when door is c and car is c, and player chooses different doors.
Your effort is to reproduce Savant's explanation.
Mine is to show errors in Savant's explanation.
That is done with a complete list of games for 1 door, playing each one by the rules, then comparing door1 with the OPtional door for any advantage.
It does not require any probabilities or repetitions of games.
Who adds 2+3 100 times to prove the result is 5?
A quote from her 1990 original answer (about age 45).
"Yes; you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened. Suppose there are a million doors, and you pick door #1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?"
Naive or lack of experience or both! She believes the probability of each door to literally be 1/M, and as the doors are opened revealing no car, their contribution is transferred to the remaining doors, finally to #777,777, but not to the door containing the car!
Just another reason for my personal philosophy,
'There are no experts, only some people with more experience than others'.
Those 1000's who disagreed with her are on my side.
Much respect, as some people invite mockery.
No, she's correct. You are wrong. But you'd best stay clear of casinos.
And you clearly need more experience, because you are wrong. As explained by numerous people in numerous different ways.
And, unfortunately for you, everyone who agrees with her is correct.
Look, you're asserting that swapping after the host has revealed an empty door (or a goat) doesn't increase your chances of winning, right? That once the host has opened that door you have a 50:50 chance of winning?
And you agree that when you pick a door at the start, you have a 1/3 chance of winning?
Okay. What you're saying is that if you don't swap then, once the host has revealed a goat, you should win 50% of the time.
So try it. Play 100 games. Pick a door and don't swap. Open one of the other doors that is empty (or has a goat) but don't swap.
Tell us the results.
Gain some of your much-loved experience, and be astounded when the more games you play, the more your win ratio trends toward 33.3%.
Don't start with the outcome and work back, but start with each game being when you pick one of the 3 doors. Because that's where (afaict) you are erring in your analysis.
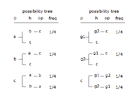
Here are the options (doors are C, G1, G2):
Pick C - don't swap - win
Pick G1 - don't swap - lose
Pick G2 - don't swap - lose
You can't decide to pick the car (C) more times than the others - it is a random choice by you, so each of those options will be picked 1/3 of the time (or at least trend toward that the more you play): you will pick C, G1, and G2 each 1/3 of the time.
Your fallacious analysis starts with the possible variations of game (there being 2 with "Pick C"), not with the initial choice. That is your mistake, since you don't take into account the different frequency of those 4 variations.
DaveC426913
Valued Senior Member
There is no such thing as a "composite game".
Rather, what has happened is that you have taken one real world result and assigned it to two slots in your theory. That should be a strong hint that your logic is not modeling the real world scenario.
I didn't "do" anything except play the game as the rules specify. It has no logic or rationale, only rules and outcomes.
The fact that you think the first game in the sim is two distinct games is damning to your argument. The first game is a whole and complete game with a valid outcome.
You're basically trying to argue that the first roll of a die turning up a 6 skews the results of the probability curve. Of course it does!
This game is a game of probabilities over multiple plays; by definition, no single game will result in perfect probability curve.
If your theory does not predict the observed outcome, then you theory is wrong. The obseved outcome is that switching increases the odds of winning.
Your objection is invalid; the data stands unchallenged. The odds for a win change when the contestant switches doors.
Last edited:
DaveC426913
Valued Senior Member
I now strongly suspect (as did many of you long ago) that phyti has given up on seeking the truth and is stuck on simply following his argument bloodyheadedly for the sake of not being able to admit he's wrong.
I consider the issue resolved. Switching doors increases the odds (i.e. over multiple plays) of winning.
Anyone who foregoes the theoretical hoop-jumping and actually plays the game will come to the same conclusion. i.e. data/observation trumps theory.
I consider the issue resolved. Switching doors increases the odds (i.e. over multiple plays) of winning.
Anyone who foregoes the theoretical hoop-jumping and actually plays the game will come to the same conclusion. i.e. data/observation trumps theory.