To claim my attempts to educate are a waste of time would make me think you think Jason.Marshall is incapable of learning or that learning is valueless or that my time is too valuable to be spend answering Jason.Marshall's questions. Is this your position? Even if it is a waste of my time, what business is it of yours who have never found value in my posts?rpenner: I don't know why you waste your time with stuff like this.
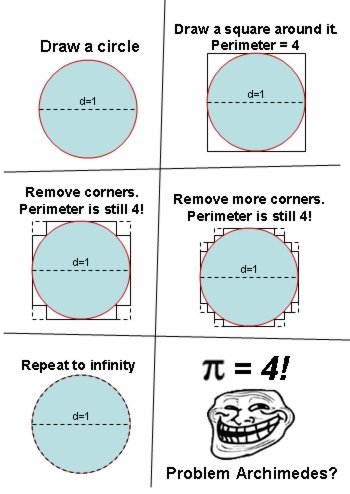
How are physical measurements, with necessarily finite precision, going to establish that the ratio of circumference to diameter is exactly π? What is needed are procedures that generalize to any level of precision. Archimedes gave us such a method, but needed regular 96-gons to demonstrate 3 + 10/71 < π < 22/7. But lots of numbers satisfy 3 + 10/71 < x < 22/7, for example: 355/113 and all numbers of the form (22 n+223)/(7 n+71) where n > 0. Today's modern methods give higher precision answers with much less labor than those of Archimedes but in doing so leave the student without connection to the geometrical problem. So I use antique methods in modern notation. Post #6 gives a result from analysis that π ≠ 3.125, post #14 gives a demonstration of how to proceed from Pythagoras via Newton to a ratio of circumference to diameter of a circle of any radius and relates that to an infinite sum of positive quantities, which prove 3.125 < π. Posts #15 and #18 demonstrate that in the limit of arbitrarily many sides, the perimeter and area of polygons approach a common behavior which is that of the circle, but also that they all share a relation of 2 A = r P. Archimedes developed the first topic:One can check that a disk is circular with say a compass, then measure its diameter and circumference.
http://itech.fgcu.edu/faculty/clindsey/mhf4404/archimedes/archimedes.html
The book is puerile and wrong, demonstrating its wrongness is not necessarily trivial depending on the education level of the reader and one would have to have only a superficial understanding of the topic to think the value of π could be settled with a single physical measurement. You have not been elected to judge Jason.Marshall for the rest of us, but instead we are all free to judge his motivation and understanding by his interactions on this forum.With facile threads like this, I wouldn't be surprised if the person asking the question was pimping his own wares.