The Monty Hall Problem Revisited

[phyti]

forum;

Game rules.
1. Host cannot open player's 1st choice door.
2. host cannot open a door containing a car.
Prizes a, b, c, can be distributed 6 possible ways.

The general game is a sequence of
1. player chooses door1.
2. host opens door2 or door3 revealing no car, eliminating it from play.
3. player chooses door1 or door op.

For the problem game,
a and b are replaced with a generic g for goats

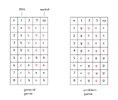
For the general game, the host has 2 possible choices for games e1 to e8.
door 1, 4c, 4g
door op, 4c, 4g
There is no advantage to switch.


For the problem game, the host has 2 possible choices for games e1 to e8.
door 1 is, 4c, 4g
door op is, 4c, 4g
There is no advantage to switch.


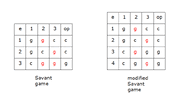
For Savant game, the host has 1 possible choice for games e1 and e2, and
2 possible choices for game e3.
door 1 is 2c, 2g
door op is 2c, 2g

There is no advantage to switch.
There is a problem with game e3. The host cannot open door2 and door3 in the same game, nor use alternate choices, which would be a different definition of a game.
Savant correctly identifies it, but does nothing to fix it.

"So let’s look at it again, remembering that the original answer defines certain conditions, the most significant of which is that the host always opens a losing door on purpose. (There’s no way he can always open a losing door by chance!)"

If e1 and e2 are played 10 times, and e3 is played 5 times revealing door2 and 5 times revealing door3, the data becomes biased.
door 1 is 10c, 20g
door op is 20c, 10g
There is an advantage to switch, but it is a fictitious one.
The fix is adding e4. The host can now open door2 or door3, and it's not a random choice.
For the modified Savant game, the host has 1 possible choice for games e1 to e4.
door1 is 2c, 2g
door op is 2c, 2g
There is no advantage to switch.
No surprise since it is half of the problem game.

The results depend on number of host choices which depends on the game rules.
The player who never knows the location of the car, can only make a random guess.
The game gives the appearance of player involvement.

 

[DaveC426913]

The game gives the appearance of player involvement.

The player is involved. The Player's involvement is, admittedly, trivial: 'always switch when the host opens a door'. The player does not need to make a decision on what to do. But only because the correct decision is always the same one.

A mechanical device that always (metaphorically) hits the "switch" button will win more often than most humans (whose fallible instincts will try to tell them occasionally to stay).

I proved this with my data. My (mechanical) script is programmed to 'always switch'. And it won twice as often as 'always staying':



So did Wiki's:



QED.

 

[phyti]

DaveC;
Savant was 1 game short!
The key factor is possible choices, not possible locations.
The host participation alters the number of choices for the player.
There are 3 possible locations for the car, but 4 possible host choices.
The key factor is possible choices, not possible locations.

This flow chart shows the 4 possible sequences of choices by following each colored path. The game rule restricting the host from opening a door containing a car, results in the same 2 choices for the player, win a car or win a goat. The win ratio is 1/2 for stay or switch.

Thanks for all the feedback. It helped to refine my paper.

 

[DaveC426913]

This flow chart shows the 4 possible sequences of choices by following each colored path. The game rule restricting the host from opening a door containing a car, results in the same 2 choices for the player, win a car or win a goat.

You are still confusing possibilities with probabilities.

The win ratio is 1/2 for stay or switch.

Then your paper is wrong.

You still ignore the fact that the data shows your ideas to be false. why do you never address this, in all the times it's been pointed out? Is it deliberate? Perhaps because you have no defense?

 

[Sarkus]

The key factor is possible choices, not possible locations.

...

The key factor is possible choices, not possible locations.

Wrong, as explained many times by many people in many ways. You can also repeat your claim as often as you want, but it won't make it any less wrong.

Each initial choice (car, goat1, goat2) has 1/3 chance of being picked. If there is only one thing the host can do from that initial choice then the outcome also 1/3 chance. If there are two things the gist could do then (assuming he chooses randomly) each possible outcome has 50% of that 1/3... i.e. 1/6 chance.

As said before, you are refusing to acknowledge the frequency of each of the host's choices, and just asserting that they are all the same. This would require the player to initially pick the car twice as often, which would invalidate the assumption that the player picks randomly.


if you really want to submit your paper for ridicule when there are such obvious mistakes that you have continually failed to address when repeatedly pointed out to you, that's your prerogative, I guess.

 

[James R]

phyti:

You're dodging my question.

Is there an error in the analysis I presented in post #125, above? If so, where did I go wrong?

Please quote the part where I made my mistake, if I made one.

This example would result in switching wins 4 of 6 times, but
this example is not all possible games.

In post #125, I explicitly listed all possible games.

You don't need me to walk you through the other two copies of my table, in which the car is initially behind door A or B rather than behind C, do you? You can see that makes no difference, I hope. (?)

What you need is all possible 6 distributions for 1 door.

I don't know what you're talking about. I think you're just trying to obfuscate, now. Look at the table I provided in post #125. I included all possible variant games and I calculated the probabilities for you.

The stay vs switch is done by comparing player door with op door.

I don't understand what you're trying to say.

Your many complex tables aren't helping. They overcomplicate things, as far as I can tell.

Why don't you try to identify the flaw you assume exists in my post #125, instead?

If you can't, then maybe there's something you haven't understood.

 

[James R]

JamesR;

Too confusing when door is c and car is c, and player chooses different doors.

If the car was behind door a instead of door c, that would just result in another table like the one in post #125, producing the same probability of a 2/3 chance for the player to win the car using the switch strategy. And if the car was behind door b instead of door c, we'd get a third table leading to the same result for a third time.

There's no loss of generality due to assuming the car is initially behind door c. There's nothing special about door c that makes it any different from door a or b.

You don't really need to see three (or maybe six?) copies of the same table of probabilities (with all six permutations of the letters ABC), do you? Or do you?

Your effort is to reproduce Savant's explanation.

No. I produced my own explanation. Several, in fact. All leading the same conclusion.

Mine is to show errors in Savant's explanation.

But you keep ignoring the probability that the player is playing each one of the possible variants.

That's your error, as I have pointed out previously.

A quote from her 1990 original answer (about age 45).

"Yes; you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened. Suppose there are a million doors, and you pick door #1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?"

Naive or lack of experience or both! She believes the probability of each door to literally be 1/M...

If there are M doors, and only 1 door has the car behind it, then the player has a 1/M chance of picking the door with the car initially.

This is basic probability, phyti.

...and as the doors are opened revealing no car, their contribution is transferred to the remaining doors, finally to #777,777, but not to the door containing the car!

Let's simplify Savant's example, because you seem to be struggling with the large number of doors. Let's make it 10 doors instead of 1 million. Only one door has a car behind it.

The player starts by picking a door at random. Do you agree that he has a 1/10 chance of randomly choosing the door with the car behind it, in this case?

Now, the host opens all doors except for two: the one the player originally chose and one other. This reveals that none of the other doors has the car behind it.

Do you agree that the player now knows for sure that the car is either behind the door he originally chose or behind the one other door that the host hasn't opened?

At this point of the game, do you think that there's now a 1/2 chance that the car is behind the door that the player didn't originally choose and a 1/2 chance that the car is behind the door that the player originally chose? If you do, then you are WRONG. Let's see why.

The player is now faced with the choice: stick with the original door he chose, or switch to the only other unopened door.

What would *you* advise the player to do now: stick or switch?

If you have agreed that the player's chances of choosing the "right" door initially were 1 in 10, then you must agree that, at the start of the game, there was a 9/10 chance that the car was behind a door other than the one he originally chose.

The car hasn't moved since the start of the game.

Suppose the player originally chose door 1. At the start of the game, there was a 1/10 chance that the car was behind door 1. That hasn't changed.

At the start of the game, there was also a 1/10 chance that the car was behind door 2, and a 1/10 chance it was behind door 3, ..., and a 1/10 chance it was behind door 10.

But the moment the host opened the first door - let's say it was door 2 - those probabilities for the unopened doors had to be re-calculated. The 1/10 probability for door 2 shrank to zero as soon as the host opened door 2. But the probabilities for doors 3 through 10 each simultaneously increased by 1/8 of 1/10, making the probability that the car was behind any given door (#3 to #10) 1/10+1/80=9/80. When the host opens door 3, again the probability that the car is behind door 1 doesn't budge: it's still 1/10. But now the probability that the car is behind doors #4 through #10 has increased by 1/7 of 1/10, bringing it up toa total of 9/80+1/70 for each door. And so on and so forth.

When there are only two doors left: the player's original choice and the only remaining door the host hasn't opened, the probability that the car is behind the player's original door is still 1/10. But the probability that the car is behind the only other unopened door has increased to 9/10.

To maximise his chances of winning the car, the player must opt to switch doors.

Going back to Savant's example with 1 million doors: the player initially has a 1 in a million chance of picking the door with the car. After the host has opened 999,998 other doors, the chances that the car is behind the only unopened door other than the one the player originally chose is 999,999 in 1 million. The player would be crazy to stick with his original door, given these odds.

Do you agree?

If you were playing the million door version of the Monty Hall game, would you stick or swap, upon being presented with the choice after the host had opened 999,998 doors?

Are you still going to insist that you think, at this point, as a player, you'd have a 1 in 2 chance of winning the car by sticking with your original choice?

If you do, I don't think anything more I can say will get through to you. I'll just have to hope that, at some point, the light bulb with go off in your muddled maths brain at some later date.

Just another reason for my personal philosophy,
'There are no experts, only some people with more experience than others'.

Those 1000's who disagreed with her are on my side.

Unfortunately for you, the thousands who disagree with vos Savant aren't very good at maths. Up until now, I thought you were pretty clued in. Maybe this is an aberration.

 

[James R]

phyti:

Just to anticipate the objection I think you'll make to the argument I made in post #147...

You'll probably want to complain that in the 10 door version of the game, I insist that the probability that the car was behind door #1 remains 1/10 at all times, while I "distribute" the remaining 9/10 probability evenly among the other doors each time the host opens one of them. Why don't I distribute some of that probability to the player's original door choice, too?

The player's initial choice of door effectively splits the entire set of doors into two distinct groups: doors that will definitely not be opened until only two doors remain unopened, and doors that might be opened before only two unopened doors remain. i.e. assuming the player picked door #1 originally, we have two groups of doors consisting of door #1 in the first group and doors #2 though #10 in the second group.

It is important to recognise that when I am speaking of "the probability that the car is behind door #N", I am actually talking about the extent of the player's knowledge about which of the remaining unopened doors the car could possibly be behind.

Initially, when the player chooses door #1 and all ten doors are closed, the player has no knowledge of what's behind any door, so the probability of the car is 1/10 for each of the ten doors.

The player gets no new information about door #1 until the location of the car is revealed at the very end of the game. Therefore, the a priori probability that the car is behind door #1 cannot change before the car's location is revealed.

But as soon as the host starts to open doors in the second group (i.e. doors other than the car door and the player's door), the player's knowledge about the doors in that group increases. When the host opens door #2 to reveal a goat, the player now knows for sure that the car isn't behind door #2. So, the original 9/10 probability (player's knowledge, remember) that the car was behind one of doors #2 through #10 must now be distributed among 8 unopened doors rather than the 9 unopened doors that were originally in the relevant group.

Continue the process and we arrive at the end-game situation: the player's knowledge about what's behind door #1 hasn't changed, because there was never any chance that the host would open door #1 prior to the endgame. But the player now has definite knowledge that 8 out of the 9 doors in the group the host could have opened do not hide the car. It follows that there is a 9/10 chance that the car is behind the only remaining unopened door in the group of doors that the host could have opened, and a 1/10 chance that the car is behind the door the player originally picked.

Now, at the endgame, the player is given the choice: "stick or switch?" The most sensible course of action is obvious.

 

[phyti]

Constant refinement reveals subtle error.

Player chooses from door table on the left.
Host choice depends on which prize is behind door1.
Host chooses from prize table on the right.

e is event/game
p is prize behind player 1st choice {door1}.
h is prize behind host choice {door2, door3}.
ad is prize behind player 2nd choice {alternate door}.


events.

1. if p is g1, h is g2, and player chooses g1 or c.
2. if p is g2, h is g1, and player chooses g2 or c.
3. if p is c, h is g1, and player chooses c or g2,
4. if p is c, h is g2, and player chooses c or g1.

When p is c, player can choose g1 or g2, NOT g1 and g2.

3 prizes, 3 locations, 4 host choices, 8 player choices
No advantage to switch from p to ad.

Since the prize table is the same for all 3 doors, the player's door choice is irrelevant!

 

[DaveC426913]

No advantage to switch from p to ad.

Then your logic is flawed.

You are defining possibilities, but you are not defining probabilities correctly.

Look, I've made this mistake before in a different problem. It's a common pitfall.

You start adding rows, one by one, mixing and matching combinations of actions and doors. But it's very easy to get mixed up in terms of the probability of a given outcome. If one event precludes a subsequent event, does it count as part of the probability?

For example:

Game	Car is behind	Player chooses door	Host opens door	Player's action	Outcome
1	1	1	2	Stay	Win
2	1	1	3?

One can immediately run into an issue here. Is game 2 a valid scenario, distinct from game 1? Does it count toward the total probability of 1?

The only way to get a trustworthy result is to run the sim and check the actual results. And the actual results demonstrate that switching results more wins.

So if your logic says otherwise, you have inadvertently included an invalid option or excluded a valid option.

 

[gmilam]

Once again, Phyti shows 4 opening "plays" when there are only 3. I'm starting to think that he's not a troll, but is in fact stupid.

 

[James R]

Constant refinement reveals subtle error.

Player chooses from door table on the left.
Host choice depends on which prize is behind door1.
Host chooses from prize table on the right.

e is event/game
p is prize behind player 1st choice {door1}.
h is prize behind host choice {door2, door3}.
ad is prize behind player 2nd choice {alternate door}.
View attachment 6703

events.

1. if p is g1, h is g2, and player chooses g1 or c.
2. if p is g2, h is g1, and player chooses g2 or c.
3. if p is c, h is g1, and player chooses c or g2,
4. if p is c, h is g2, and player chooses c or g1.

When p is c, player can choose g1 or g2, NOT g1 and g2.

3 prizes, 3 locations, 4 host choices, 8 player choices
No advantage to switch from p to ad.

Since the prize table is the same for all 3 doors, the player's door choice is irrelevant!

You made the same error here, again.

Look at your "prize" table. In that table, there are 4 possible ways the game can play out. However, two thirds of the time, the player will be playing either game 1 or game 2. The player will only play either game 3 or 4 one third of the time (which also means, of course, that the player will play game 3 one sixth of the time, and game 4 one sixth of the time).

In games 1 and 2, the player wins the car by switching. That happens in two-thirds of all games.
In games 3 and 4, the player loses by switching. That happens in one-third of all games.

Therefore, once again, your conclusion is incorrect and Marilyn vos Savant (and the rest of us - me, Sarkus, etc.) are all correct.

Your mistake - which you keep making, despite the error being pointed out to over and over in slightly different ways - is that you assume that all 4 game variants in your "prize" are equally likely. They are not.

Will you finally accept that you made a mistake, or are you going to continue to try to defend the indefensible?

 

[James R]

Then your logic is flawed.

Indeed. phyti hasn't analysed the problem correctly.

You are defining possibilities, but you are not defining probabilities correctly.

Correct.

The only way to get a trustworthy result is to run the sim and check the actual results. And the actual results demonstrate that switching results more wins.

I have given the correct analysis in about three different ways in this thread. No sim is needed to verify my analysis. It's equivalent to a mathematical proof. If the premises are correct and each logical step in the derivation of the result is correct, then the argument is logically sound.

This does not mean that running a simulation is worthless, however. I'm sure that phyti could write a simple program to run the simulation of the Monty Hall game as it is actually played. If he did, he would obviously get the same results you got.

But he doesn't want to do that, apparently. Nor does he want to be honest about addressing the flaws in his own "proof", which have been pointed out several times by different people in this thread.

This is uncharacteristically obtuse for phyti, who is usually on the ball when it comes to maths. Maybe, at this point, it's a matter of misguided pride or something. Whatever is going on in his head, it isn't a careful consideration of the arguments that have been made against his analysis or in favour of the correct analysis of the problem.

As a last-ditch effort, I have now engaged with him by referring to his own notation and preferred way of thinking about the problem. I have explained exactly where his error lies. It seems to me, that in the face of a direct disproof of his reasoning, he must admit he was wrong, if he is really the rational, clear thinker he usually presents as.

If he cannot amid his error at this point, I think I'll have to write him off as a lost cause, on this particular topic at least. Maybe it's a kind of mental break that's confined solely to this particular problem, for whatever reason. Or maybe he has just spent too long being emotionally invested in the wrong answer.